21 Apr Nodal Stress Calculation
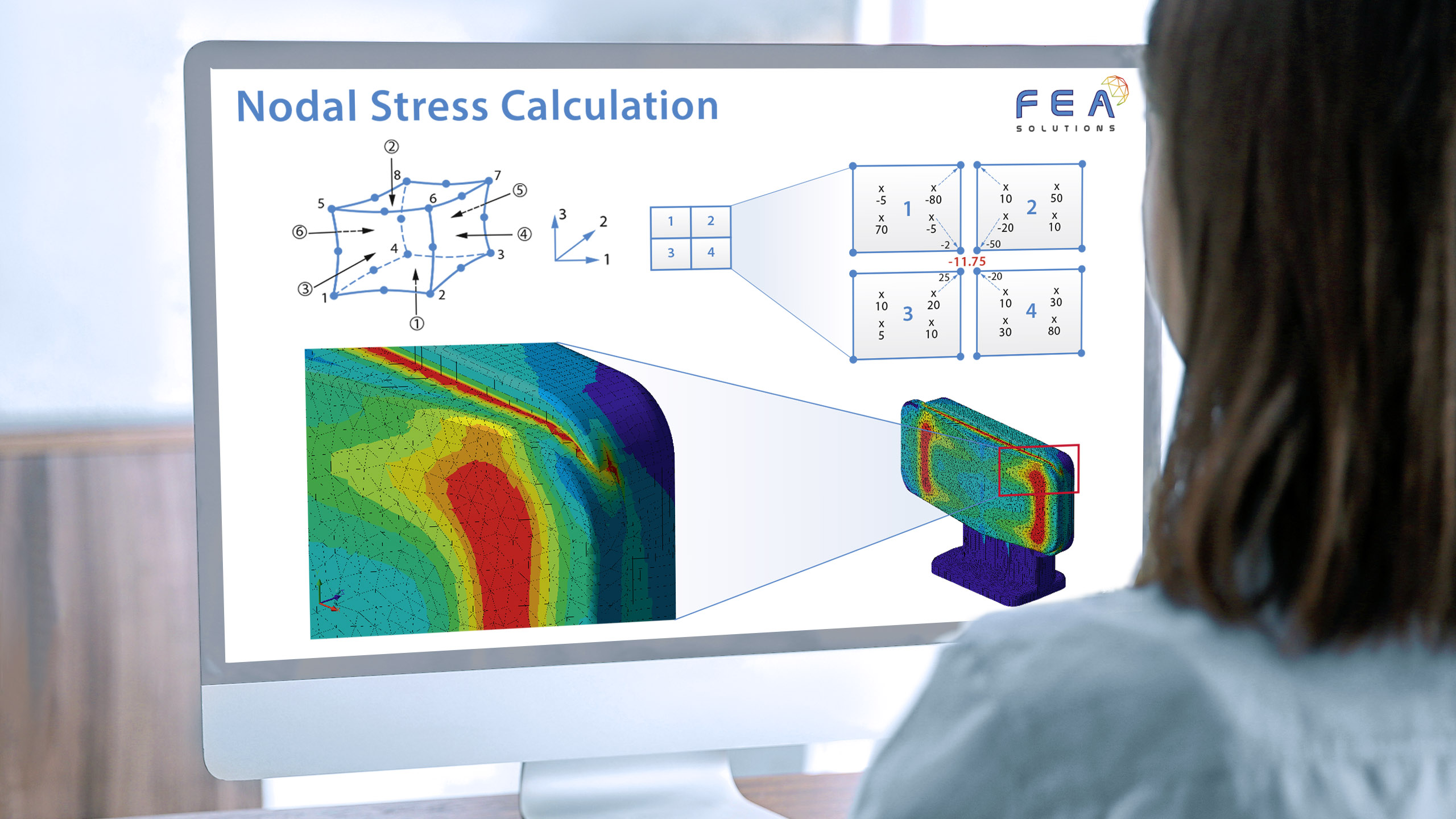
During the static stress analysis of a structure, FEA solves its stiffness matrix. The results of this solution are nodal displacements. That means a FEA stress analysis is actually a displacement analysis. The nodal displacement results are precise, that means each node within the mesh (https://fea-solutions.co.uk/fea-terminology/) has just one nodal displacement.
In the next step of the FEA, element stresses are calculated based on the displacements of all nodes that define one particular element. The stresses are calculated at so-called integration points or Gaussian Points, which are inside of the element, not right at the nodes. These results are then extrapolated out to the nodes. Hence, if in a FEA mesh two (or more) elements share the same node, the stresses that each of these elements are extrapolating to that node are usually not the same, despite being in the same physical location within the structure. To come up with a nodal stress, the common procedure is to calculate the average (https://fea-solutions.co.uk/stress-averaging/) of the extrapolated element stresses at that node.
Nodal displacement results are precise. Nodal stress results can be accurate, depending on the mesh size, but they are never precise. This is true for solid elements (https://fea-solutions.co.uk/solid-elements/), partly true for plate elements (https://fea-solutions.co.uk/surface-elements/) but not applicable to beam elements (https://fea-solutions.co.uk/line-elements/), because these three are based on completely different mathematical models.
Please give us a call today on +44 (0)1202 798991 to discuss any engineering analysis requirements you might have.
