01 Feb Scalar, Vector and Matrix
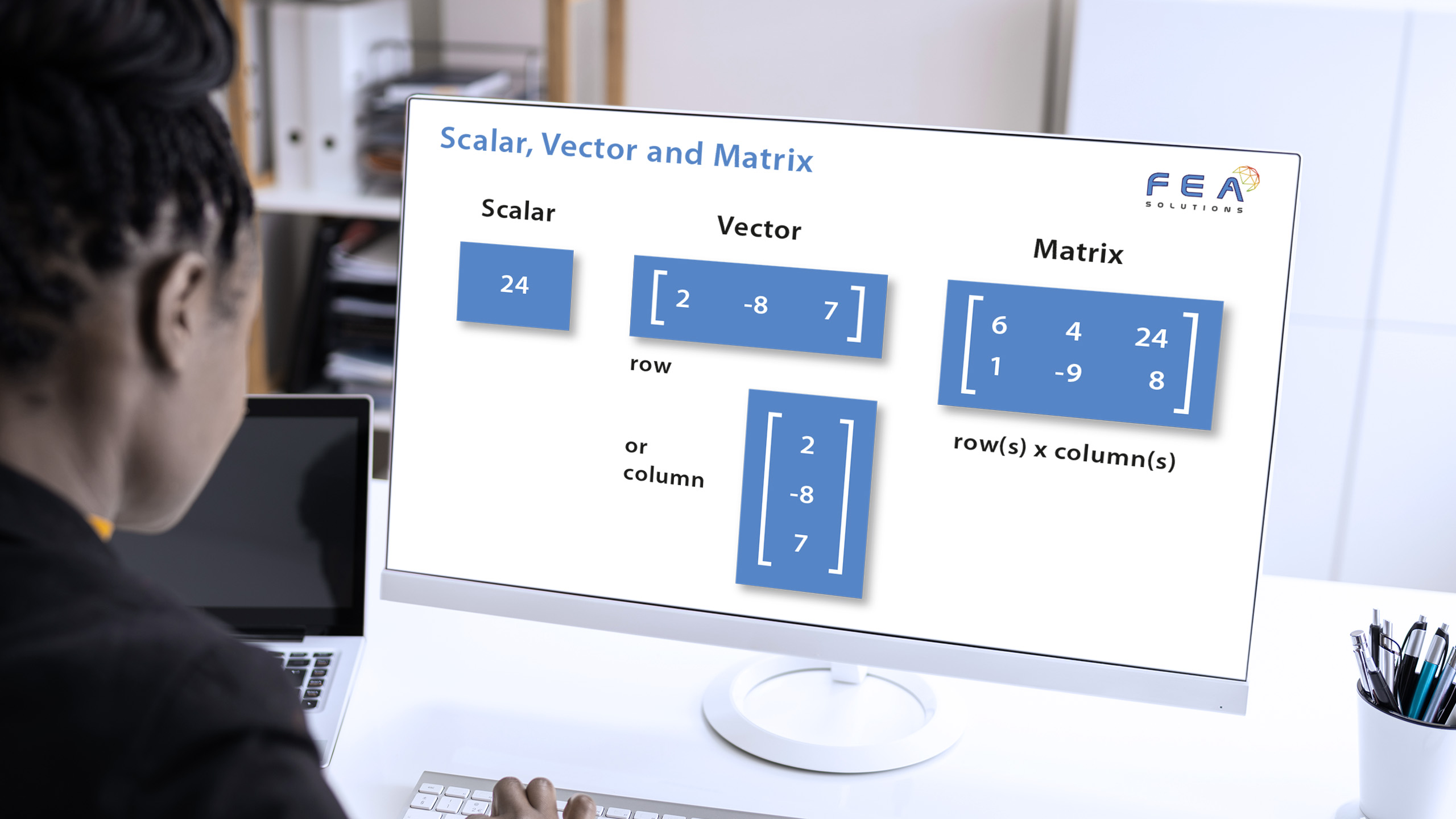
In mathematics, all values can be represented by either a scalar, a vector or a matrix.
A scalar is a quantity which is fully defined by a magnitude. In engineering, examples of scalars include mass (https://fea-solutions.co.uk/mass-and-weight/), energy and time.
A vector is a quantity which is fully defined by a magnitude and a direction. In engineering, examples of vectors include velocities, accelerations, forces and moments (https://fea-solutions.co.uk/force-and-moment-symbols/). A vector can be depicted as an arrow, with its length being the magnitude. Vectors can be defined in either two-dimensional space (2D) or three-dimensional space (3D).
A matrix (sometimes called an array) is a quantity which is fully defined by a number of magnitudes in a number of directions. A matrix with m columns and n rows is called a m by n matrix, with m and n being the dimensions. Matrices can be defined in either 2D or 3D. In engineering, examples of matrices include the stiffness, mass and damping matrices which are solved within a structural FEA model. They are always n x n matrices.
Please call us today on +44 (0)1202 798991 for any engineering analysis requirements you might have.
