11 May Element Order
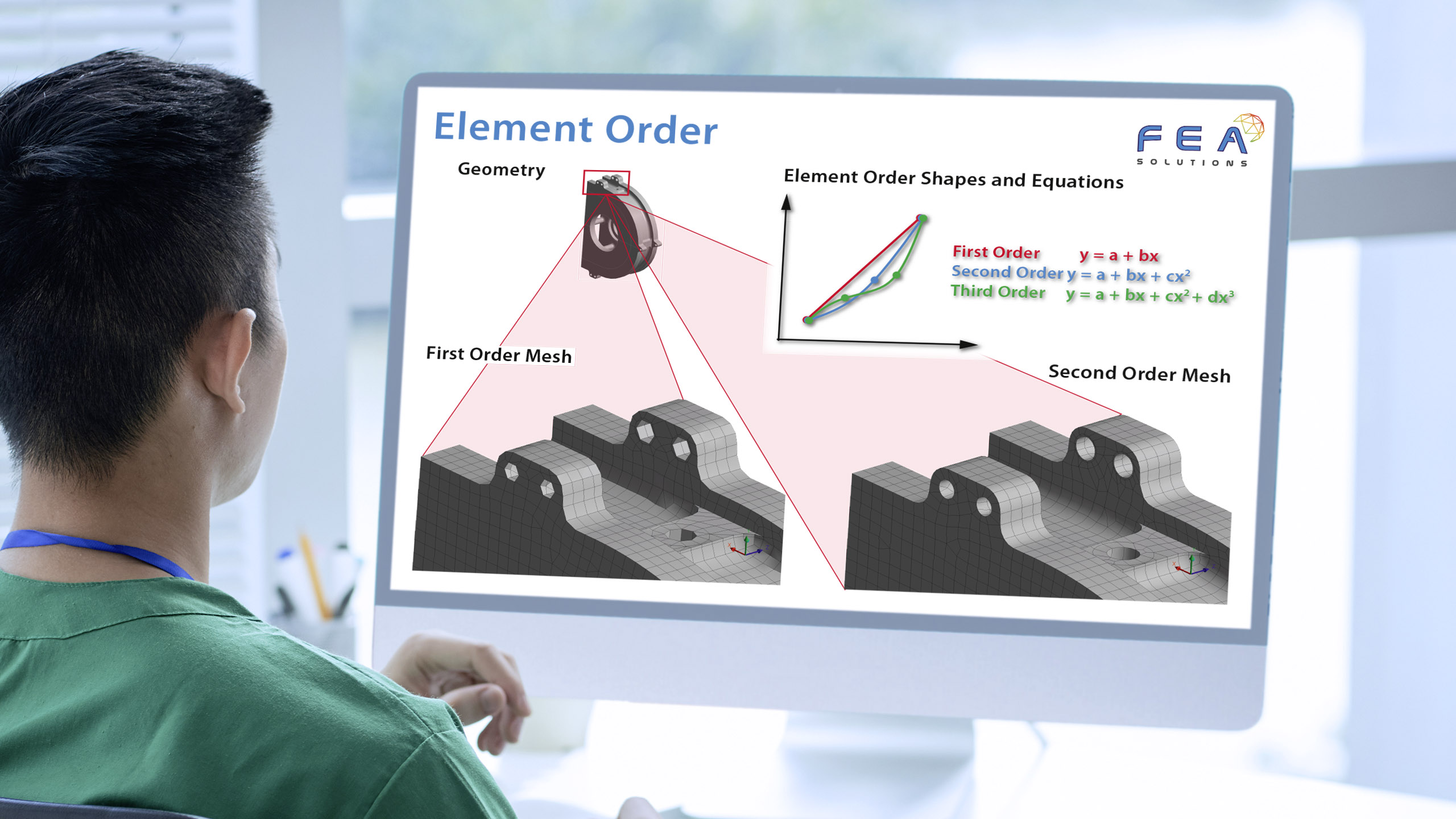
When meshing a geometry in FEA, the resulting elements (https://fea-solutions.co.uk/fea-terminology/) used are defined not only by their type (https://fea-solutions.co.uk/fea-element-types/), but also by their order. The order of element describes how many nodes are on an element edge. 1st order elements have nodes only at the corners of their edges. Higher order elements also have nodes at points along the element edges, so called mid-side nodes. They are usually only available for solid elements.
The element order defines the shape of the element edge. The edge of a 1st order element can only be a straight line, whereas higher order elements can have curved edges.
That is why higher order elements provide more accurate results compared to 1st order elements of the same size. This is because they have more complex equations to represent the shapes the edges, and thus have more degrees of freedom. For the first three element orders, the polynomial equations describing them are the following:
– 1st Order: y = a + bx, representing a straight line, hence also called linear element.
– 2nd Order: y = a + bx + cx², representing a parabolic curve, hence also called parabolic element
– 3rd Order: y = a + bx + cx² + dx³, representing a s-curve
First order elements are the cheapest elements to use computationally, but offer the worst representation of a curved geometry compared to higher order elements, due to the lack of mid-side nodes.
Most FEA software can handle 2nd order elements in addition to 1st order elements. Some packages can also generate higher order elements.
Please call us today on +44 (0)1202 798991 for any engineering analysis requirements you might have.
